会员朋友们大家好,我是成都荒原书店主理人、前北京科技大学物理系教师季燕江,欢迎大家关注《给普通人的量子力学》,希望能和大家一起感受物理的魅力。
阅读往期可点击:
物理学中可以严格求解的模型很少,弹簧振子是其中之一。
在经典物理学中,假设我们有一根弹簧,弹簧本身的质量忽略不计,弹簧末端挂着一个质量为m的物体。由于重力和弹簧弹力可以互相抵消,弹簧可以静止下来。此时物理系统的能量最小。
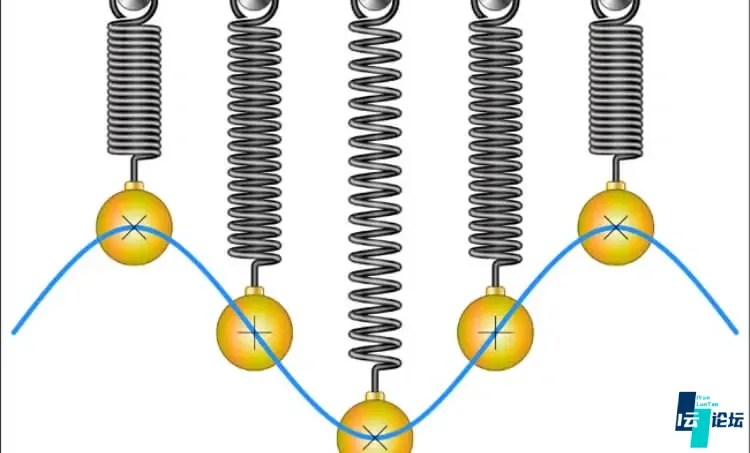
假设我移动物体,使其偏离平衡位置,弹簧会对物体施加一个弹性回复力,这个力的大小和物体偏离平衡位置的位移成正比,方向相反,表示为:-kx。
换句话说,我们是在与弹簧的弹力相对抗的状态下才偏离了位移x。这就好比爬山,我们是在与重力对抗的状态下升高了h。即:我们都在做功,使系统的势能升高了。所谓势能(potential energy)就是潜在的可以对外做功的能力,拉伸弹簧或者抬升物体其实就是在储能。
弹簧是人类最早的储能技术,应用在弩等器械上。对生命来说,是通过糖来储能的,而在日常生活中,我们一般是用电池来储能的。

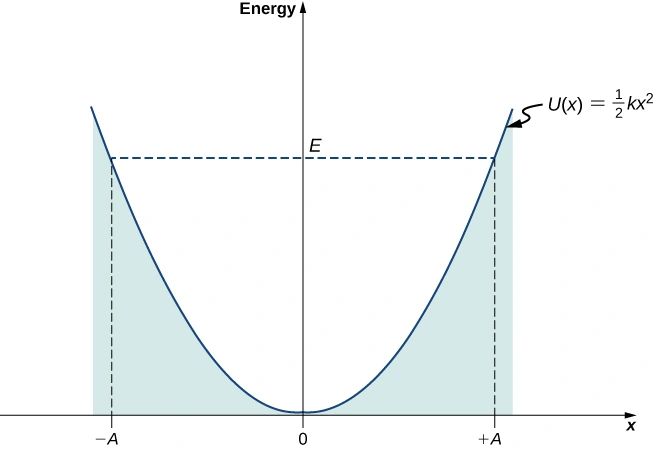
物体偏离平衡位置x,储存起来的势能U(x)是kx²/2。物体还具有动能:mv²/2,这一项我们常改写为含动量p的形式,p²/2m。
总能量就是:
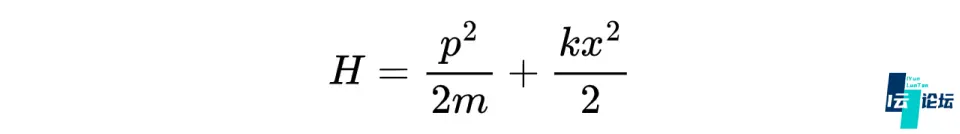
经典物理学中,最直接的求解弹簧振子运动的方法是使用牛顿第二定律(F = ma):
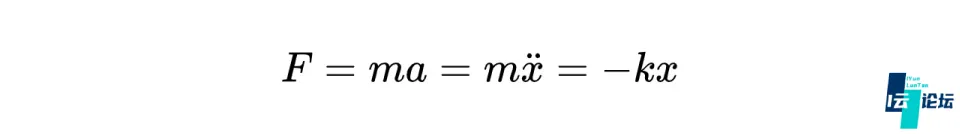
这对应一个二阶微分方程:
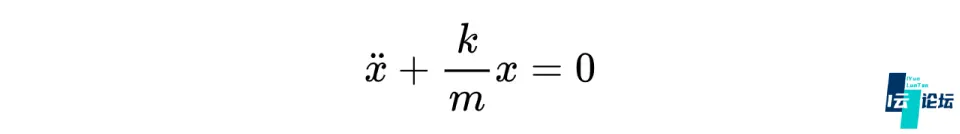
这个方程的解是一个简谐振动,振动的频率满足:
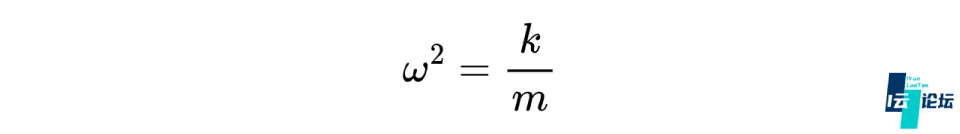
现在用mω²替代弹性系数k,弹簧振子一般用如下哈密顿量描述:
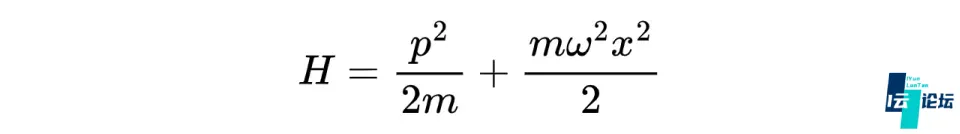
弹簧振子的经典解,我们暂时就讨论到这里,重点展开量子力学对弹簧的求解。
免责声明:如果侵犯了您的权益,请联系站长,我们会及时删除侵权内容,谢谢合作! |